- Autor Matthew Elmers [email protected].
- Public 2023-12-16 22:31.
- Modificat ultima dată 2025-01-24 09:34.

Ce determină acuratețea - una dintre caracteristicile principale ale unei arme? Evident, din calitatea butoiului și a cartușului. Să amânăm cartușul pentru moment, dar luăm în considerare fizica procesului.
Luați o tijă sau un tub metalic din metal elastic și fixați-l rigid într-o bază masivă. Deci, obținem un model al dispozitivului în studiu. Acum, dacă lovim tija, nu contează în ce loc și în ce direcție, fie o trageți înapoi, fie o strângeți, fie, în cele din urmă, introducând un cartuș în tub și tragând o lovitură, vom vedea că tija (butoiul) a intrat într-o mișcare oscilatorie amortizată. Aceste vibrații sunt descompuse în cele mai simple, iar fiecare tip de vibrație atât de simplă a butoiului va afecta precizia (acuratețea) fotografierii în felul său.
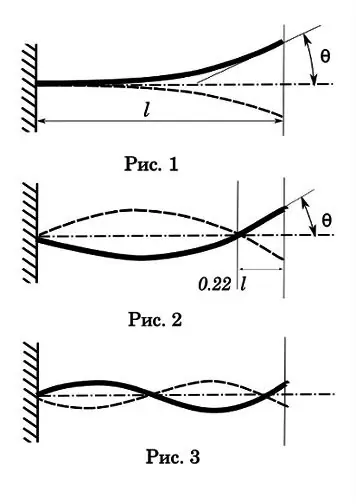
Să începem cu vibrațiile de prim ordin sau de înălțime. După cum puteți vedea (Fig. 1), o astfel de oscilație are un singur nod la punctul de atașare, cea mai mare amplitudine, cel mai lung timp de decădere și cel mai lung timp de oscilație dintr-o perioadă. Acest timp este de 0,017-0,033 sec. Timpul de călătorie a glonțului prin foraj este de 0, 001-0, 002 sec. Adică, semnificativ mai puțin decât ciclul unei oscilații, ceea ce înseamnă că acest tip de oscilație nu are un efect semnificativ asupra preciziei unei singure fotografii. Dar, cu fotografierea automată, se poate dovedi o imagine interesantă. Să presupunem că rata de foc este de 1200 rds / min, adică timpul unui ciclu - 0,05 sec. Cu o perioadă de oscilație de prim ordin de 0, 025 sec, avem un raport de frecvență multiplu. Și aceasta este o condiție indispensabilă pentru rezonanță cu toate consecințele care rezultă - arma începe să tremure cu o forță atât de mare încât să se poată destrăma.
Să trecem la oscilații de ordinul doi (Fig. 2). Dar sugerez studenților din domeniul științelor umaniste să efectueze mai întâi un experiment pentru a elimina neajunsurile educației în domeniul fizicii. Trebuie să iei un băiețel (poți o fată), să-l pui pe leagăn și leagăn. Înainte de tine este un pendul. Stai în lateralul leagănului și încearcă să-l lovești pe băiat cu mingea. După o serie de încercări, veți ajunge la concluzia că cel mai bun mod de a lovi este atunci când ținta se află în prima fază a oscilației - abaterea maximă de la punctul de echilibru. În acest moment, ținta are viteză zero.
Să ne uităm la diagrama de ordinul doi. Al doilea nod de vibrații este situat la aproximativ 0,22 de la capătul butoiului. Acest punct este o lege a naturii, este imposibil să se creeze astfel de vibrații pentru fasciculul în consolă, astfel încât al doilea nod să cadă pe capătul liber. Este locul unde este și nu depinde de lungimea butoiului.
Amplitudinea oscilației pentru schema de ordinul doi este mai mică, dar timpul de oscilație este deja comparabil cu timpul de trecere a glonțului prin alezaj - 0, 0025-0, 005 sec. Deci, pentru fotografierea simplă, acest lucru este deja interesant. Pentru a clarifica despre ce vorbim, imaginați-vă un butoi lung de 1 metru. Glonțul traversează întregul butoi în 0, 001 secunde. Dacă perioada de oscilație este de 0,004 sec, atunci până când glonțul părăsește butoiul, butoiul va atinge îndoirea maximă în prima fază. Întrebarea pentru științe umane este - în ce moment (în ce fază) este cel mai bine să tragi un glonț din butoi pentru a asigura coerența rezultatelor? Amintiți-vă leagănul. În punctul zero, vectorul vitezei de deviere a trunchiului este maxim. Este mai dificil pentru un glonț să atingă acest punct pe butonul tăiat, are și propria eroare de viteză. Adică, cel mai bun moment pentru ca glonțul să zboare afară va fi atunci când butoiul se află în cel mai înalt punct al primei faze de deviere - ca în figură. Apoi, abaterile nesemnificative ale vitezei glonțului vor fi compensate de timpul mai lung petrecut de butoi în faza sa cea mai stabilă.
O reprezentare grafică a acestui fenomen poate fi văzută clar în diagramă (Fig. 4-5). Aici - ist este eroarea de timp cu care glonțul traversează botul butoiului. În fig. 4 este ideal atunci când timpul mediu de decolare a glonțului coincide cu faza zero a oscilației barilului. (Matematicieni! Știu că distribuția vitezei este neliniară.) Zona umbrită este unghiul de răspândire a traiectoriilor.
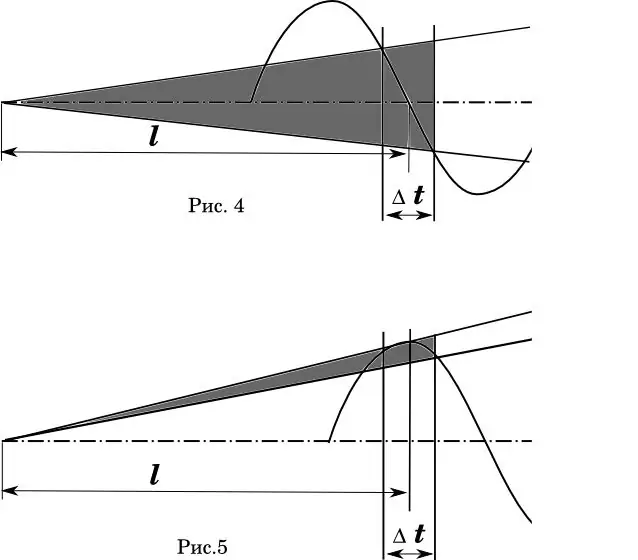
În Fig. 5, lungimea cilindrului și eroarea de viteză rămân aceleași. Dar faza de îndoire a butoiului este deplasată astfel încât timpul mediu de plecare să coincidă cu devierea maximă a butoiului. Comentariile sunt de prisos?
Ei bine, merită lumânarea? Cât de grave pot fi abaterile cauzate de oscilațiile de ordinul doi? Serios și foarte serios. Potrivit profesorului sovietic Dmitry Aleksandrovich Ventzel, într-unul dintre experimente s-au obținut următoarele rezultate: raza abaterii mediane a crescut cu 40% cu o modificare a lungimii barilului cu doar 100 mm. Pentru comparație, o procesare de înaltă calitate a butoiului poate îmbunătăți precizia cu doar 20%!
Acum să aruncăm o privire la formula pentru frecvența vibrațiilor:
Unde:
k - coeficient pentru oscilații de ordinul doi - 4, 7;
L este lungimea barilului;
E este modulul de elasticitate;
I este momentul de inerție al secțiunii;
m este masa trunchiului.
… și continuați cu analiza și concluziile.
Concluzia evidentă din figurile 4-5 este eroarea de viteză a glonțului. Depinde de calitatea pulberii și de greutatea și densitatea acesteia din cartuș. Dacă această eroare este de cel puțin un sfert din timpul ciclului, atunci orice altceva poate fi renunțat. Din fericire, știința și industria au atins o stabilitate foarte mare în această chestiune. Și pentru cei mai sofisticați (de exemplu, în banchetă) există toate condițiile pentru auto-asamblarea cartușelor pentru a regla faza de eliberare a glonțului exact la lungimea cilindrului.
Deci, avem un cartuș cu cea mai mică variație de viteză posibilă. Lungimea barilului a fost calculată pe baza greutății sale maxime. Se pune problema stabilității. Ne uităm la formulă. Ce variabile afectează schimbarea frecvenței oscilației? Lungimea cilindrului, modulul de elasticitate și masă. Butoiul se încălzește în timpul arderii. Poate schimba căldura lungimea cilindrului, astfel încât precizia să fie afectată. Da și nu. Da, deoarece această cifră se află la sute de procente pentru o temperatură de 200 C. Nu, deoarece modificarea modulului elastic al oțelului pentru aceeași temperatură este de aproximativ 8-9%, pentru 600C este aproape de două ori. Adică de multe ori mai mare! Butoiul devine mai moale, faza de îndoire a butoiului se deplasează înainte în momentul în care pleacă glonțul, precizia scade. Ei bine, ce spune un analist atent? El va spune că este imposibil să obțineți o precizie maximă pe o lungime de butoi în modul rece și cald! Arma poate avea o performanță mai bună cu un butoi rece sau fierbinte. În consecință, se obțin două clase de arme. Unul este pentru acțiunile de ambuscadă, când ținta trebuie lovită de la prima lovitură „rece”, deoarece acuratețea celei de-a doua va fi mai proastă din cauza încălzirii inevitabile a butoiului. Într-o astfel de armă nu este nevoie urgentă de automatizare. Și a doua clasă este puștile automate, a căror lungime a butoiului este ajustată la butoiul fierbinte. În acest caz, o posibilă ratare datorită preciziei scăzute a unei lovituri reci poate fi compensată printr-o lovitură rapidă mai caldă și mai precisă.
EF Dragunov cunoștea foarte bine fizica acestui proces când își proiecta pușca. Vă sugerez să vă familiarizați cu povestea fiului său Alexei. Dar mai întâi, cineva va trebui să-și rupă creierul. După cum știți, două mostre de Konstantinov și Dragunov s-au apropiat de finala competiției pentru o pușcă de lunetă. Designerii au fost prieteni și s-au ajutat reciproc în toate. Deci, pușca lui Konstantinov a fost „reglată” la modul rece, pușca lui Dragunov la „fierbinte”. Încercând să îmbunătățească acuratețea puștii rivalei, Dragunov își trage pușca cu pauze lungi.

Să privim din nou formula. După cum puteți vedea, frecvența depinde și de masa butoiului. Masa trunchiului este constantă. Dar contactul dur cu forendul produce un feedback pozitiv imprevizibil la butoi. Sistemul - țeavă-for-braț (suport) va avea un moment diferit de inerție (un set de mase în raport cu punctul de atașare), ceea ce înseamnă că acest lucru poate provoca și o schimbare de fază. Acesta este motivul pentru care sportivii folosesc un suport moale. Aceeași caracteristică este asociată cu aplicarea principiului „țeava suspendată”, atunci când partea frontală a armei nu are un contact dur cu țeava și este atașată rigid la aceasta (arma) numai în zona receptor, iar al doilea capăt fie nu atinge deloc butoiul, fie atinge printr-o îmbinare cu arc (SVD).
Gândul final. Faptul că, cu aceeași lungime a butoiului, este imposibil să obțineți aceeași precizie la temperaturi diferite, oferă un motiv excelent pentru a vă întinde creierul. Este necesar să schimbați lungimea și / sau masa butoiului numai atunci când temperatura butoiului se schimbă. Fără a schimba nici lungimea, nici greutatea butoiului. Din punct de vedere al științelor umaniste, acesta este un paradox. Din punctul de vedere al unui tehnician, o sarcină ideală. Întreaga viață a unui designer este legată de soluționarea unor astfel de probleme. Sherlock-urile se odihnesc.






